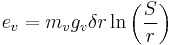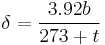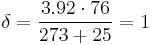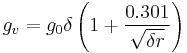Peek's law

In physics, Peek's law is a description of the conditions necessary for corona discharge between two wires:

e_v = m_v g_v \delta r \ln \left ({S \over r} \right )

ev is the "visual critical corona voltage" or "corona inception voltage" (CIV), the voltage (in kilovolts) required to initiate a visible corona discharge between the wires.

mv is an irregularity factor to account for the condition of the wires. For smooth, polished wires, mv = 1. For roughened, dirty or weathered wires, 0.98 to 0.93, and for cables, 0.87 to 0.83.

r is the radius of the wires

S is the distance between the wires

δ is the air density factor. It is calculated by the equation:

\delta = {3.92 b \over 273 %2B t}
where
  • b = pressure in centimeters of mercury
  • t = temperature in degrees Celsius
At SATP (25°C and 76 cmHg):
\delta = {3.92\cdot76 \over 273 %2B 25} = 1

gv is the "visual critical" potential gradient, and is calculated by the equation:

g_v = g_0 \delta \left ( 1 %2B {0.301 \over \sqrt{\delta r}} \right )
where g0 is the "disruptive critical" potential gradient, about 30 kV/cm for air [1]

References

  1. ^ Hong, Alice (2000). "Electric Field to Produce Spark in Air (Dielectric Breakdown)". The Physics Factbook. http://hypertextbook.com/facts/2000/AliceHong.shtml.